简介

MaAsLin 2 是 MaAsLin（微生物组多变量线性模型关联，Microbiome Multivariable Association with Linear Models）的下一代产品。

MaAsLin 2 是一个全面的 R 语言软件包，用于高效地确定表型、环境、暴露、协变量和微生物组元组学特征之间的多变量关联。MaAsLin 2 依赖于一般线性模型来适应大多数现代流行病学研究设计，包括横断面和纵向研究，以及多种数据探索、标准化和转换方法。

安装

1
2
3

if(!requireNamespace("BiocManager", quietly = TRUE))
    install.packages("BiocManager")
BiocManager::install("Maaslin2")

微生物组关联检测

输入文件

微生物组特征数据或功能数据

• 以制表符分隔列
• 行为样本，列为特征（微生物/基因/功能……）

元数据

• 以制表符分隔列
• 行为样本，列为特征

两个文件包含的样本可以不同，分析时只取二者共有的样本。样本顺序也无需一致。

读入文件

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

df_input_data = read.table(file             = input_data,
                           header           = TRUE,
                           sep              = "\t", 
                           row.names        = 1,
                           stringsAsFactors = FALSE)
df_input_data[1:5, 1:5]

df_input_metadata = read.table(file             = input_metadata, 
                               header           = TRUE, 
                               sep              = "\t", 
                               row.names        = 1,
                               stringsAsFactors = FALSE)
df_input_metadata[1:5, ]

df_input_path = read.csv("./pathabundance_relab.tsv", 
                         sep              = "\t", 
                         stringsAsFactors = FALSE, 
                         row.names        = 1)
df_input_path[1:5, 1:5]

运行MaAsLin 2

在MaAsLin中，可以使用几种不同类型的统计模型来进行关联测试（例如简单线性模型、零膨胀模型、基于计数的模型等）。作者在论文中评估了各种模型的优缺点，虽然默认模型通常适用于大多数分析，但在某些情况下，用户可能希望选择不同的模型。这同样适用于多种不同的微生物群落数据类型（taxonomy 或functional profiles）、环境（人类或其他）和测量方式（计数或相对比例），只要使用适当修改过的归一化/转换方案即可。

对于模型选择，如果你的输入是计数数据，那么你可以使用NEGBIN和ZINB模型；而对于非计数数据（如百分比、CPM或相对丰度）的输入，你可以使用LM和CPLM模型。

在MaAsLin 2实现的归一化方法中，TMM和CSS仅适用于计数数据，并且它们也返回归一化后的计数，这与TSS和CLR不同。因此，如果你的输入是计数数据，你可以使用上述两种归一化方法（即TMM、CSS或NONE（如果数据已经归一化））而无需进一步转换（即transform = NONE）。

在非计数模型中，CPLM要求数据为正数。因此，任何产生负值的转换通常都不适用于CPLM。

由于所有非LM模型都与其与广义线性模型（GLM）的紧密联系而使用固有的对数链接转换，因此建议它们以transform = NONE的方式运行。

除此之外，LM是唯一能够处理正数和负数（在归一化/转换之后）的模型，并且（根据手稿）它通常对参数变化具有更强的鲁棒性（这是非LM模型的典型限制）。关于是否使用LM、CPLM或其他模型，直观上，在存在零值的情况下，CPLM或零膨胀替代模型应该表现更好，但根据我们的基准测试，我们没有证据表明CPLM显著优于LM模型。因此，在选择模型时，应综合考虑数据的特性、研究目的以及模型的适用性和性能。

注：通常，还需要考虑用于过滤数据（即流行率和丰度阈值）的阈值，以减少异常值和假阳性。有关此方面的更多详细信息，请参阅MaAsLin 2中的第4.3.1节“流行率和丰度过滤”。

以下命令在HMP2数据上运行MaAsLin 2，执行多变量回归模型以测试微生物物种丰度与IBD诊断和菌群失调评分之间的关联（fixed_effects = c("diagnosis", "dysbiosis")）。对于具有超过2个水平的任何分类变量，还需要指定哪个变量应作为参考水平，方法是使用（reference = c("diagnosis,nonIBD")）。注：在变量和水平之间添加空格可能会导致使用错误的参考水平。输出将生成在当前工作目录下的名为demo_output的文件夹中（output = "demo_output"）。在此示例中，输入数据已预先进行归一化和过滤，因此我们也将关闭默认的归一化和流行率过滤。

1
2
3
4
5
6
7

fit_data = Maaslin2(input_data     = df_input_data, 
                    input_metadata = df_input_metadata, 
                    min_prevalence = 0,
                    normalization  = "NONE",
                    output         = "demo_output", 
                    fixed_effects  = c("diagnosis", "dysbiosis"),
                    reference      = c("diagnosis,nonIBD"))

输出

重要关联

MaAsLin 2最重要的输出之一可能是重要关联的列表。这些关联在significant_results.tsv文件中提供：

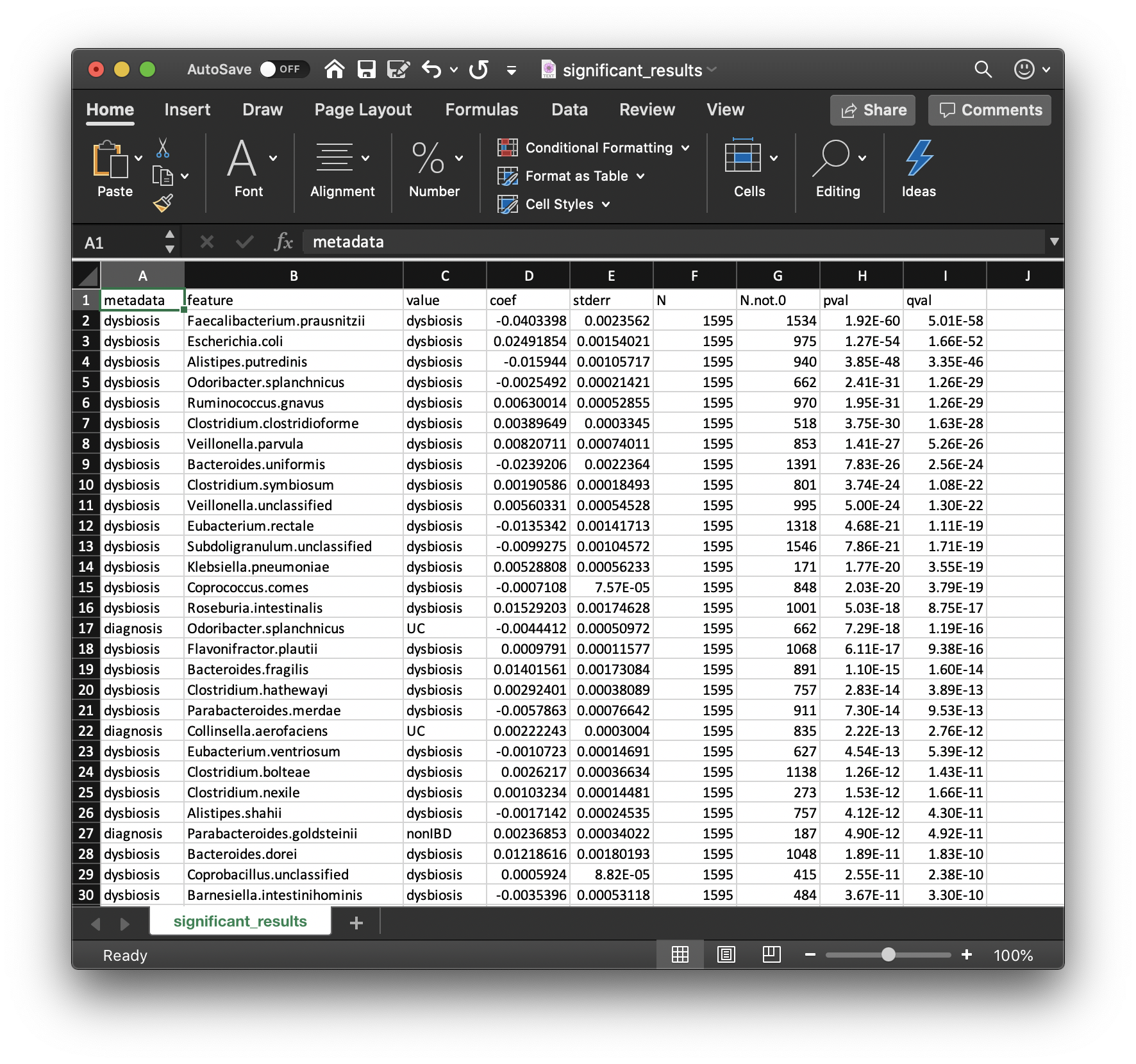
这些是通过MaAsLin 2显著性阈值的全部关联列表，按照q值递增的顺序排序。列包括：

• metadata：与微生物特征相关联的变量名。

• feature：微生物特征（分类群、基因、途径等）。

• value：对于分类特征，这是报告系数和关联显著性的具体特征水平。

• coef：模型系数值（效应大小）。对于分类变量，系数表示在value中指定的类别与参考类别之间的对比。

• stderr：模型的标准误差。

• N：用于此关联的模型中样本的总数（例如，因为可以排除缺失值）。

• N.not.0：在这些样本中，特征非零的总数。

• pval：此关联的名义显著性。

• qval：使用p.adjust函数和校正方法（如BH等）计算得到的校正显著性。

• 问题：如何解释这个表格的第一行？

对于significant_results.tsv中的每个重要关联，MaAsLin 2还会生成可视化图表以供检查（分类变量的箱线图，连续变量的散点图）。这些图表命名为“metadata_name.pdf”。例如，从我们的分析运行中，我们得到了可视化文件dysbiosis.pdf和diagnosis.pdf。

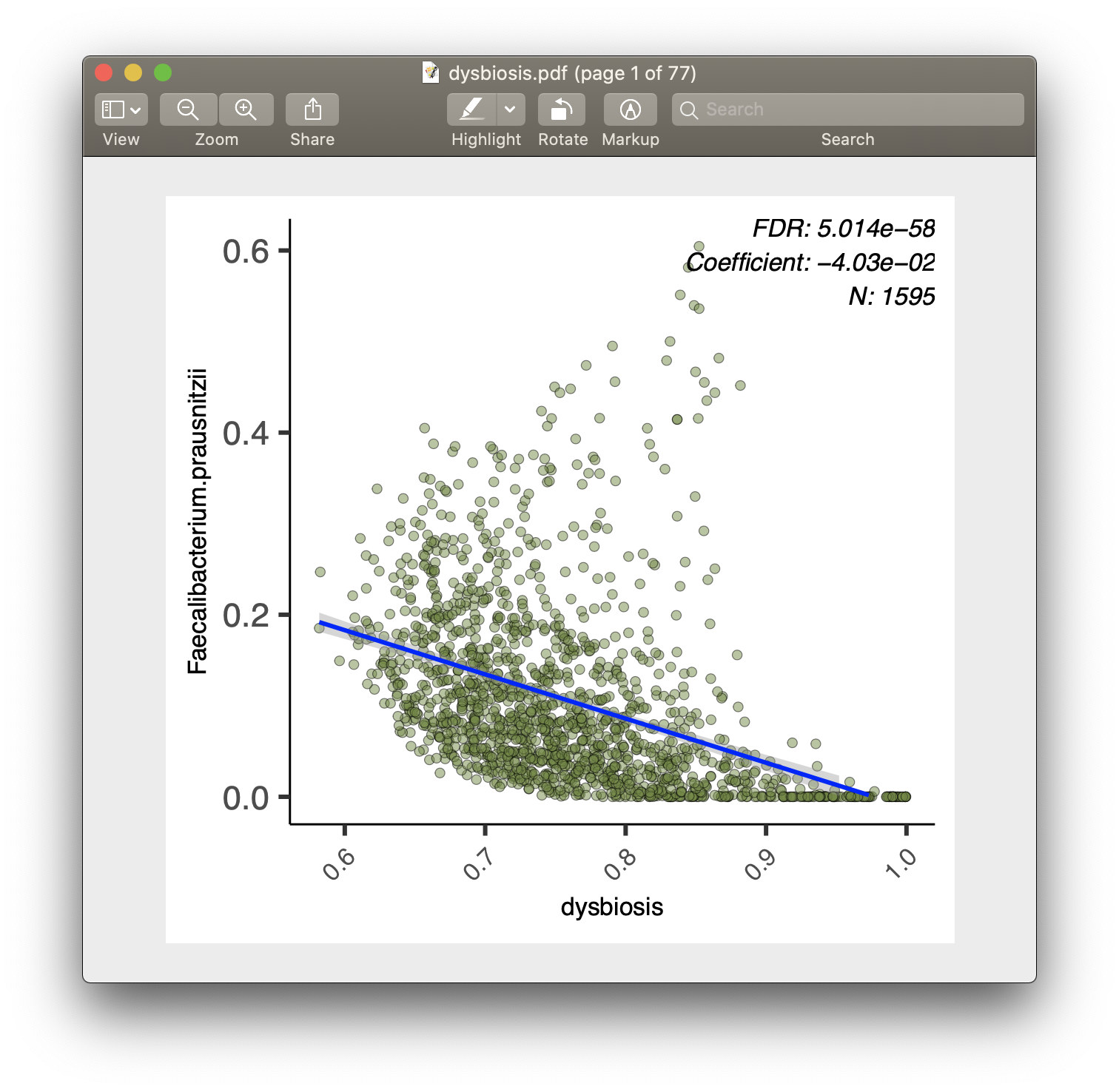
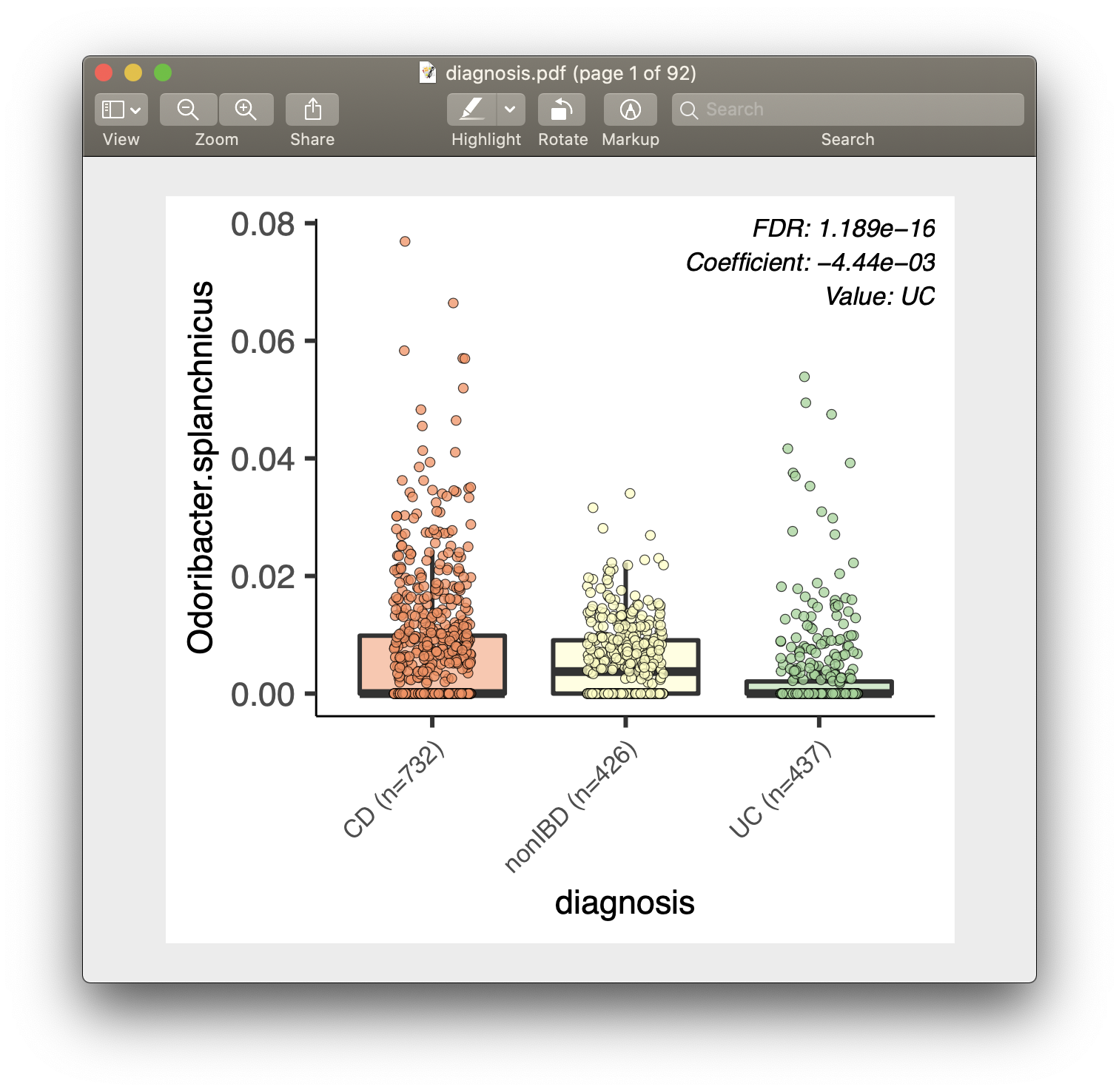
输出文件完整列表

MaAsLin 2生成两种类型的输出文件：数据和可视化文件。

• 数据输出文件

  • significant_results.tsv

  • all_results.tsv

    • 与significant_results.tsv格式相同，但包含所有关联结果（而不仅仅是显著的结果）。
    • 您也可以在R中使用fit_data$results访问此表。

  • residuals.rds

    • 此文件包含一个包含每个特征残差的数据框。

  • maaslin2.log

    • 此文件包含运行的所有日志信息。
    • 它包括所有设置、警告、错误和运行的步骤。

• 可视化输出文件

  • heatmap.pdf

    • 此文件包含显著关联的热图。

  • [a-z/0-9]+.pdf

    • 为每个显著关联生成一个图表。
    • 对于连续元数据，使用散点图。
    • 对于分类数据，使用箱线图。
    • 绘制的数据点已经过归一化、过滤和转换。

MaAsLin 2在功能谱上的应用

如果您的功能表是由HUMAnN生成的，并且已经使用humann_renorm_table脚本进行了归一化，那么您不需要执行任何额外的归一化——测序深度的影响已经被消除（这正是本教程中将使用的）。我们倾向于使用CPM单位，因为我们发现它们更方便，但在建模目的上，它们在数值上与相对丰度是等价的（CPM = RA * 1e6）。

否则，可使用上述关于模型/归一化/转换的相同思路。

在使用MaAsLin 2处理功能谱时的一些其他快速提示：

• 为了减少特征数量，通常希望运行未分层的功能特征（或分层特征的过滤子集）。
• 可能还想移除与特定分类群高度相关的功能特征（即可能由该微生物贡献），因为这些特征可以通过分类学变化得到更好的解释。

1
2
3
4
5
6
7

#This can also be done with with the HUMAnN 3 untiliy `humann_split_stratified_table`
unstrat_pathways <-function(dat_path){
  temp = dat_path[!grepl("\\|",rownames(dat_path)),]
  return(temp)
}

df_input_path = unstrat_pathways(df_input_path)

在由bioBakery工作流程生成的MetaCyc途径表上运行与上述相同的模型。

1
2
3
4
5
6
7

fit_func = Maaslin2(input_data     = df_input_path, 
                    input_metadata = df_input_metadata, 
                    output         = "demo_functional", 
                    fixed_effects  = c("diagnosis", "dysbiosis"),
                    reference      = c("diagnosis,nonIBD"),
                    min_abundance  = 0.0001,
                    min_prevalence = 0.1)

注意：在这里，我们有列中的样本和行中的特征，MaAsLin 2正确地识别了这一点，并且能够匹配样本。

作者最近还发表了关于使用MaAsLin 2分析宏转录组学数据（MTX）中差异特征的研究，有关该主题的更多信息，请参阅最近的出版物。

高级主题

交互作用

许多统计分析都关注于测试某些变量之间的交互作用。不幸的是，MaAsLin 2目前尚未提供直接的界面来进行此操作。相反，用户需要创建人工交互列作为额外的fixed_effects项。以上面的拟合为例，为了测试诊断与菌群失调之间的交互作用，我可以创建两列额外的数据：CD_dysbiosis和UC_dysbiosis（因为诊断的参考是非IBD）。

1
2
3
4
5
6
7
8
9
10
11
12

df_input_metadata$CD_dysbiosis = (df_input_metadata$diagnosis == "CD") *
                                 df_input_metadata$dysbiosis
df_input_metadata$UC_dysbiosis = (df_input_metadata$diagnosis == "UC") *
                                 df_input_metadata$dysbiosis

fit_data_ixn = Maaslin2(input_data     = df_input_data, 
                        input_metadata = df_input_metadata, 
                        min_prevalence = 0,
                        normalization  = "NONE",
                        output         = "demo_output_interaction", 
                        fixed_effects  = c("diagnosis", "dysbiosis", "CD_dysbiosis", "UC_dysbiosis"), 
                        reference      = c("diagnosis,nonIBD"))

随机效应

某些研究自然地将样本观测值“分组”，例如在纵向设计中按受试者分组或在家庭设计中按家庭分组。对于统计分析来说，重要的是要处理属于同一组的样本之间的非独立性。MaAsLin 2 通过 random_effects 参数提供了一个简单的界面来处理这个问题，用户可以在其中指定分组变量来运行混合效应模型。例如，我们注意到 HMP2 是一个纵向设计，其中同一个受试者（列中的 subject）可以有多个样本。因此，我们要求 MaAsLin 2 使用 subject 作为其随机效应分组变量：

1
2
3
4
5
6
7
8

fit_data_random = Maaslin2(input_data     = df_input_data, 
                           input_metadata = df_input_metadata, 
                           min_prevalence = 0,
                           normalization  = "NONE",
                           output         = "demo_output_random", 
                           fixed_effects  = c("diagnosis", "dysbiosis"),
                           random_effects = c("subject"),
                           reference      = c("diagnosis,nonIBD"))

如果你对在纵向研究中测试时间的影响感兴趣，那么在调用 MaAsLin 2 时，时间点变量应该包含在 fixed_effects 中。

• 问题：直觉上，你能想到为什么解决样本之间的非独立性很重要吗？
  • 提示：想象一下一个简单的场景，你有两个受试者，一个病例和一个对照，每个受试者都有两个样本。
  • 当同一受试者的样本高度独立时，与它们高度相关时，有效样本大小是多少？

其他选项

MaAsLin 2 提供了许多参数选项，用于不同的数据预处理（规范化、过滤、转换）和其他任务。这些选项的完整列表是：

• min_abundance

  • 每个特征的最小丰度 [ 默认值：0 ]

• min_prevalence

  • 以最小丰度检测到一个特征的最小样本百分比 [ 默认值：0.1 ]

• max_significance

  • 显著性的 q 值阈值 [ 默认值：0.25 ]

• normalization

  • 要应用的规范化方法 [ 默认值：”TSS” ] [ 选项：”TSS”、”CLR”、”CSS”、”NONE”、”TMM” ]

• transform

  • 要应用的转换 [ 默认值：”LOG” ] [ 选项：”LOG”、”LOGIT”、”AST”、”NONE” ]

• analysis_method

  • 要应用的分析方法 [ 默认值：”LM” ] [ 选项：”LM”、”CPLM”、”ZICP”、”NEGBIN”、”ZINB” ]

• correction

  • 计算 q 值的校正方法 [ 默认值：”BH” ]

• standardize

  • 应用 z 分数，以便连续元数据在同一尺度上 [ 默认值：TRUE ]

• plot_heatmap

  • 为显著关联生成热图 [ 默认值：TRUE ]

• heatmap_first_n

  • 在热图中，绘制具有显著关联的前 N 个特征 [ 默认值：50 ]

• plot_scatter

  • 为显著关联生成散点图 [ 默认值：TRUE ]

• cores

  • 并行运行的 R 进程数 [ 默认值：1 ]

• reference

  • 用作具有两个以上级别的变量的参考，以“变量,参考”的字符串形式提供，多个变量之间用分号分隔。

MaAsLin 2 中的流行率和丰度过滤

通常，只有在某个特征在“足够”多的时间内非零时，测试特征与元数据之间的关联才有意义。“足够”的具体比例可能因研究而异，但 10-50% 的最小流行率阈值并不罕见（高达 70-90% 也是合理的）。由于我们已经在使用一小部分精选的演示数据，我们将使用 min_prevalence = 0.1 来仅测试至少 10% 的非零值的特征。请注意：这是 MaAsLin 2 中的默认参数设置。

类似地，通常只希望测试在这么多样本中达到最小丰度阈值的特征。默认情况下，MaAsLin 2 会认为任何非零值都是可靠的，如果你已经在数据集中进行了充分的质量控制（QC），那么这样做是合适的。然而，如果你想要进行更多过滤或采取保守态度，你可以设置一个最小丰度阈值，如 min_abundance = 0.0001，以仅测试达到这个（相对）丰度的特征。

将这些参数组合起来，我们可以使用两者来运行 MaAsLin 2（并且速度会更快！）：

1
2
3
4
5
6
7
8
9

fit_data_filter = Maaslin2(input_data     = df_input_data, 
                           input_metadata = df_input_metadata, 
                           normalization  = "NONE",
                           output         = "demo_output_filter", 
                           fixed_effects  = c("diagnosis", "dysbiosis"),
                           reference      = c("diagnosis,nonIBD"),
                           random_effects = c("subject"),
                           min_prevalence = 0.1,
                           min_abundance  = 0.0001)

命令行

1

Maaslin2.R --transform=AST --fixed_effects="diagnosis,dysbiosis"  /usr/local/lib/R/site-library/Maaslin2/extdata/HMP2_taxonomy.tsv /usr/local/lib/R/site-library/Maaslin2/extdata/HMP2_metadata.tsv demo_output --reference="diagnosis,nonIBD"

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66

$ Maaslin2.R --help
Usage: ./R/Maaslin2.R [options] <data.tsv> <metadata.tsv> <output_folder>

Options:
    -h, --help
        Show this help message and exit

    -a MIN_ABUNDANCE, --min_abundance=MIN_ABUNDANCE
        The minimum abundance for each feature [ Default: 0 ]

    -p MIN_PREVALENCE, --min_prevalence=MIN_PREVALENCE
        The minimum percent of samples for which a feature 
        is detected at minimum abundance [ Default: 0.1 ]

    -s MAX_SIGNIFICANCE, --max_significance=MAX_SIGNIFICANCE
        The q-value threshold for significance [ Default: 0.25 ]

    -n NORMALIZATION, --normalization=NORMALIZATION
        The normalization method to apply [ Default: TSS ]
        [ Choices: TSS, CLR, CSS, NONE, TMM ]

    -t TRANSFORM, --transform=TRANSFORM
        The transform to apply [ Default: LOG ]
        [ Choices: LOG, LOGIT, AST, NONE ]

    -m ANALYSIS_METHOD, --analysis_method=ANALYSIS_METHOD
        The analysis method to apply [ Default: LM ]
        [ Choices: LM, CPLM, NEGBIN, ZINB ]

    -r RANDOM_EFFECTS, --random_effects=RANDOM_EFFECTS
        The random effects for the model, comma-delimited
        for multiple effects [ Default: none ]

    -f FIXED_EFFECTS, --fixed_effects=FIXED_EFFECTS
        The fixed effects for the model, comma-delimited
        for multiple effects [ Default: all ]

    -c CORRECTION, --correction=CORRECTION
        The correction method for computing the 
        q-value [ Default: BH ]

    -z STANDARDIZE, --standardize=STANDARDIZE
        Apply z-score so continuous metadata are 
        on the same scale [ Default: TRUE ]

    -l PLOT_HEATMAP, --plot_heatmap=PLOT_HEATMAP
        Generate a heatmap for the significant 
        associations [ Default: TRUE ]

    -i HEATMAP_FIRST_N, --heatmap_first_n=HEATMAP_FIRST_N
        In heatmap, plot top N features with significant 
        associations [ Default: TRUE ]

    -o PLOT_SCATTER, --plot_scatter=PLOT_SCATTER
        Generate scatter plots for the significant
        associations [ Default: TRUE ]

    -e CORES, --cores=CORES
        The number of R processes to run in parallel
        [ Default: 1 ]

    -r REFERENCE, --reference='VARIABLE,REFERENCE'
        The factor to use as a reference for a 
        variable with more than two levels 
        provided as a string of 'variable,reference' 
        semi-colon delimited for multiple variables.

参考文献

• Mallick H, Rahnavard A, McIver LJ, Ma S, Zhang Y, Nguyen LH, Tickle TL, Weingart G, Ren B, Schwager EH, Chatterjee S, Thompson KN, Wilkinson JE, Subramanian A, Lu Y, Waldron L, Paulson JN, Franzosa EA, Bravo HC, Huttenhower C (2021). Multivariable Association Discovery in Population-scale Meta-omics Studies. PLoS Computational Biology, 17(11):e1009442.

加关注