前言

PCA的全称是Principal Component Analysis，即主成分分析。这是一种常用的数据分析方法，主要用于数据降维。PCA的主要思想是将原始的高维特征空间通过线性变换投射到一个新的低维特征空间上，同时尽量保持原始数据的方差，使得在新的低维空间中数据的差异性得以保留。这一过程中，通过计算数据集的协方差矩阵，找到其特征值和特征向量，进而确定主成分的方向和贡献率，实现数据的有效降维。

具体来说，PCA的计算过程包括以下几个步骤：

数据标准化：将原始数据转换为均值为0，标准差为1的标准化数据，以消除不同量纲对分析结果的影响。
计算协方差矩阵：标准化后的数据矩阵的协方差矩阵反映了各变量之间的相关性。
计算特征值和特征向量：对协方差矩阵进行特征值分解，得到特征值和对应的特征向量。特征值的大小反映了对应主成分的重要性，而特征向量则指示了主成分的方向。
选取主成分：根据特征值的大小，选取前k个主成分，使得这k个主成分的累计贡献率达到一定的阈值（如80%或90%）。
转换数据到新的主成分空间：将原始数据转换到由选定的主成分构成的新空间中，得到降维后的数据。

PCA在数据分析和机器学习领域有着广泛的应用，如特征提取、数据压缩、噪声消除、图像识别等。同时，PCA也是一种无监督学习的方法，它不需要数据的标签信息，就可以从数据中提取出有用的特征信息。

本文通过鸢尾花数据集演示PCA方法，讲解如何确定降维采用的特征向量的数量，并完成降维。包括手写函数实现和通过SK-learn实现代码。

导入数据集

import numpy as np
import pandas as pd
url = 'https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data'
df = pd.read_csv(url)
df.head()

	5.1	3.5	1.4	0.2	Iris-setosa
0	4.9	3.0	1.4	0.2	Iris-setosa
1	4.7	3.2	1.3	0.2	Iris-setosa
2	4.6	3.1	1.5	0.2	Iris-setosa
3	5.0	3.6	1.4	0.2	Iris-setosa
4	5.4	3.9	1.7	0.4	Iris-setosa

# 添加列名，分别为 sepal_len, sepal_wid, petal_len, petal_wid, class
# 前四列为特征，最后一列为类别，共有3种类别
df.columns=['sepal_len', 'sepal_wid', 'petal_len', 'petal_wid', 'class']
df.head()

	sepal_len	sepal_wid	petal_len	petal_wid	class
0	4.9	3.0	1.4	0.2	Iris-setosa
1	4.7	3.2	1.3	0.2	Iris-setosa
2	4.6	3.1	1.5	0.2	Iris-setosa
3	5.0	3.6	1.4	0.2	Iris-setosa
4	5.4	3.9	1.7	0.4	Iris-setosa

# 拆分特征和标签

X = df.iloc[:,0:4].values
y = df.iloc[:,4].values

特征工程

特征展示

查看特征的取值范围以及其和类别的关系。

# 导入matplotlib库中的pyplot模块，用于绘图
from matplotlib import pyplot as plt
# 导入math库
import math

# 定义一个字典，映射数字到鸢尾花的种类名称
label_dict = {1: 'Iris-Setosa',
              2: 'Iris-Versicolor',
              3: 'Iris-Virgnica'}

# 定义一个字典，映射数字到鸢尾花的特征名称
feature_dict = {0: 'sepal length [cm]',
                1: 'sepal width [cm]',
                2: 'petal length [cm]',
                3: 'petal width [cm]'}

# 创建一个8x6英寸的图像
plt.figure(figsize=(8, 6))
# 循环绘制4个子图，每个子图代表一个特征的直方图
for cnt in range(4):
    # 在图像中创建2x2的子图，并指定当前子图的位置
    plt.subplot(2, 2, cnt+1)
    # 遍历每种鸢尾花类别，绘制直方图
    for lab in ('Iris-setosa', 'Iris-versicolor', 'Iris-virginica'):
        # 绘制指定特征的直方图，使用不同颜色和透明度区分不同类别
        plt.hist(X[y==lab, cnt],
                 label=lab,
                 bins=10,
                 alpha=0.3,)
    # 设置子图的x轴标签
    plt.xlabel(feature_dict[cnt])
    # 添加图例，用于标识不同类别的鸢尾花
    plt.legend(loc='upper right', fancybox=True, fontsize=8)

# 调整子图间的间距，使布局更加紧凑
plt.tight_layout()
# 显示绘制的图像
plt.show()

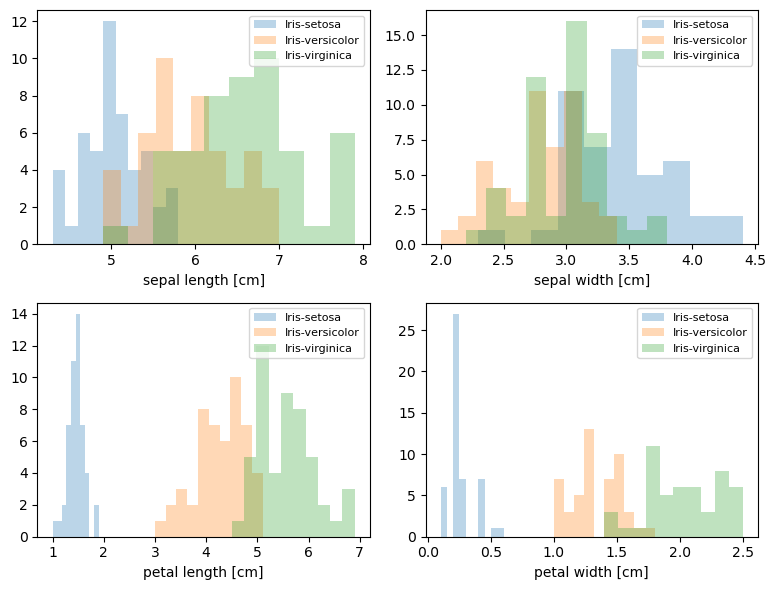
发现花萼的长度和宽度能够较好的区分3种类别。
四个特征取值范围差异较大，需要进行标准化。

数据标准化

# 进行数据标准化
from sklearn.preprocessing import StandardScaler
X_std = StandardScaler().fit_transform(X)
print (X_std)

[[-1.1483555  -0.11805969 -1.35396443 -1.32506301]
 [-1.3905423   0.34485856 -1.41098555 -1.32506301]
 [-1.51163569  0.11339944 -1.29694332 -1.32506301]
 [-1.02726211  1.27069504 -1.35396443 -1.32506301]
 [-0.54288852  1.9650724  -1.18290109 -1.0614657 ]
 [-1.51163569  0.8077768  -1.35396443 -1.19326436]
 [-1.02726211  0.8077768  -1.29694332 -1.32506301]
 [-1.75382249 -0.34951881 -1.35396443 -1.32506301]
 [-1.1483555   0.11339944 -1.29694332 -1.45686167]
 [-0.54288852  1.50215416 -1.29694332 -1.32506301]
 [-1.2694489   0.8077768  -1.23992221 -1.32506301]
 [-1.2694489  -0.11805969 -1.35396443 -1.45686167]
 [-1.87491588 -0.11805969 -1.52502777 -1.45686167]
 [-0.05851493  2.19653152 -1.46800666 -1.32506301]
 [-0.17960833  3.122368   -1.29694332 -1.0614657 ]
 [-0.54288852  1.9650724  -1.41098555 -1.0614657 ]
 [-0.90616871  1.03923592 -1.35396443 -1.19326436]
 [-0.17960833  1.73361328 -1.18290109 -1.19326436]
 [-0.90616871  1.73361328 -1.29694332 -1.19326436]
 [-0.54288852  0.8077768  -1.18290109 -1.32506301]
 [-0.90616871  1.50215416 -1.29694332 -1.0614657 ]
 [-1.51163569  1.27069504 -1.58204889 -1.32506301]
 [-0.90616871  0.57631768 -1.18290109 -0.92966704]
 [-1.2694489   0.8077768  -1.06885886 -1.32506301]
 [-1.02726211 -0.11805969 -1.23992221 -1.32506301]
 [-1.02726211  0.8077768  -1.23992221 -1.0614657 ]
 [-0.78507531  1.03923592 -1.29694332 -1.32506301]
 [-0.78507531  0.8077768  -1.35396443 -1.32506301]
 [-1.3905423   0.34485856 -1.23992221 -1.32506301]
 [-1.2694489   0.11339944 -1.23992221 -1.32506301]
 [-0.54288852  0.8077768  -1.29694332 -1.0614657 ]
 [-0.78507531  2.42799064 -1.29694332 -1.45686167]
 [-0.42179512  2.65944976 -1.35396443 -1.32506301]
 [-1.1483555   0.11339944 -1.29694332 -1.45686167]
 [-1.02726211  0.34485856 -1.46800666 -1.32506301]
 [-0.42179512  1.03923592 -1.41098555 -1.32506301]
 [-1.1483555   0.11339944 -1.29694332 -1.45686167]
 [-1.75382249 -0.11805969 -1.41098555 -1.32506301]
 [-0.90616871  0.8077768  -1.29694332 -1.32506301]
 [-1.02726211  1.03923592 -1.41098555 -1.19326436]
 [-1.63272909 -1.73827353 -1.41098555 -1.19326436]
 [-1.75382249  0.34485856 -1.41098555 -1.32506301]
 [-1.02726211  1.03923592 -1.23992221 -0.79786838]
 [-0.90616871  1.73361328 -1.06885886 -1.0614657 ]
 [-1.2694489  -0.11805969 -1.35396443 -1.19326436]
 [-0.90616871  1.73361328 -1.23992221 -1.32506301]
 [-1.51163569  0.34485856 -1.35396443 -1.32506301]
 [-0.66398191  1.50215416 -1.29694332 -1.32506301]
 [-1.02726211  0.57631768 -1.35396443 -1.32506301]
 [ 1.39460583  0.34485856  0.52773232  0.25652088]
 [ 0.66804545  0.34485856  0.41369009  0.38831953]
 [ 1.27351244  0.11339944  0.64177455  0.38831953]
 [-0.42179512 -1.73827353  0.12858453  0.12472222]
 [ 0.78913885 -0.58097793  0.47071121  0.38831953]
 [-0.17960833 -0.58097793  0.41369009  0.12472222]
 [ 0.54695205  0.57631768  0.52773232  0.52011819]
 [-1.1483555  -1.50681441 -0.27056327 -0.27067375]
 [ 0.91023225 -0.34951881  0.47071121  0.12472222]
 [-0.78507531 -0.81243705  0.07156341  0.25652088]
 [-1.02726211 -2.43265089 -0.15652104 -0.27067375]
 [ 0.06257847 -0.11805969  0.24262675  0.38831953]
 [ 0.18367186 -1.96973265  0.12858453 -0.27067375]
 [ 0.30476526 -0.34951881  0.52773232  0.25652088]
 [-0.30070172 -0.34951881 -0.09949993  0.12472222]
 [ 1.03132564  0.11339944  0.35666898  0.25652088]
 [-0.30070172 -0.11805969  0.41369009  0.38831953]
 [-0.05851493 -0.81243705  0.18560564 -0.27067375]
 [ 0.42585866 -1.96973265  0.41369009  0.38831953]
 [-0.30070172 -1.27535529  0.07156341 -0.1388751 ]
 [ 0.06257847  0.34485856  0.58475344  0.78371551]
 [ 0.30476526 -0.58097793  0.12858453  0.12472222]
 [ 0.54695205 -1.27535529  0.64177455  0.38831953]
 [ 0.30476526 -0.58097793  0.52773232 -0.00707644]
 [ 0.66804545 -0.34951881  0.29964787  0.12472222]
 [ 0.91023225 -0.11805969  0.35666898  0.25652088]
 [ 1.15241904 -0.58097793  0.58475344  0.25652088]
 [ 1.03132564 -0.11805969  0.69879566  0.65191685]
 [ 0.18367186 -0.34951881  0.41369009  0.38831953]
 [-0.17960833 -1.04389617 -0.15652104 -0.27067375]
 [-0.42179512 -1.50681441  0.0145423  -0.1388751 ]
 [-0.42179512 -1.50681441 -0.04247882 -0.27067375]
 [-0.05851493 -0.81243705  0.07156341 -0.00707644]
 [ 0.18367186 -0.81243705  0.75581678  0.52011819]
 [-0.54288852 -0.11805969  0.41369009  0.38831953]
 [ 0.18367186  0.8077768   0.41369009  0.52011819]
 [ 1.03132564  0.11339944  0.52773232  0.38831953]
 [ 0.54695205 -1.73827353  0.35666898  0.12472222]
 [-0.30070172 -0.11805969  0.18560564  0.12472222]
 [-0.42179512 -1.27535529  0.12858453  0.12472222]
 [-0.42179512 -1.04389617  0.35666898 -0.00707644]
 [ 0.30476526 -0.11805969  0.47071121  0.25652088]
 [-0.05851493 -1.04389617  0.12858453 -0.00707644]
 [-1.02726211 -1.73827353 -0.27056327 -0.27067375]
 [-0.30070172 -0.81243705  0.24262675  0.12472222]
 [-0.17960833 -0.11805969  0.24262675 -0.00707644]
 [-0.17960833 -0.34951881  0.24262675  0.12472222]
 [ 0.42585866 -0.34951881  0.29964787  0.12472222]
 [-0.90616871 -1.27535529 -0.44162661 -0.1388751 ]
 [-0.17960833 -0.58097793  0.18560564  0.12472222]
 [ 0.54695205  0.57631768  1.2690068   1.70630611]
 [-0.05851493 -0.81243705  0.75581678  0.91551417]
 [ 1.51569923 -0.11805969  1.21198569  1.17911148]
 [ 0.54695205 -0.34951881  1.04092235  0.78371551]
 [ 0.78913885 -0.11805969  1.15496457  1.31091014]
 [ 2.12116622 -0.11805969  1.61113348  1.17911148]
 [-1.1483555  -1.27535529  0.41369009  0.65191685]
 [ 1.75788602 -0.34951881  1.44007014  0.78371551]
 [ 1.03132564 -1.27535529  1.15496457  0.78371551]
 [ 1.63679263  1.27069504  1.32602791  1.70630611]
 [ 0.78913885  0.34485856  0.75581678  1.04731282]
 [ 0.66804545 -0.81243705  0.869859    0.91551417]
 [ 1.15241904 -0.11805969  0.98390123  1.17911148]
 [-0.17960833 -1.27535529  0.69879566  1.04731282]
 [-0.05851493 -0.58097793  0.75581678  1.57450745]
 [ 0.66804545  0.34485856  0.869859    1.4427088 ]
 [ 0.78913885 -0.11805969  0.98390123  0.78371551]
 [ 2.24225961  1.73361328  1.6681546   1.31091014]
 [ 2.24225961 -1.04389617  1.78219682  1.4427088 ]
 [ 0.18367186 -1.96973265  0.69879566  0.38831953]
 [ 1.27351244  0.34485856  1.09794346  1.4427088 ]
 [-0.30070172 -0.58097793  0.64177455  1.04731282]
 [ 2.24225961 -0.58097793  1.6681546   1.04731282]
 [ 0.54695205 -0.81243705  0.64177455  0.78371551]
 [ 1.03132564  0.57631768  1.09794346  1.17911148]
 [ 1.63679263  0.34485856  1.2690068   0.78371551]
 [ 0.42585866 -0.58097793  0.58475344  0.78371551]
 [ 0.30476526 -0.11805969  0.64177455  0.78371551]
 [ 0.66804545 -0.58097793  1.04092235  1.17911148]
 [ 1.63679263 -0.11805969  1.15496457  0.52011819]
 [ 1.87897942 -0.58097793  1.32602791  0.91551417]
 [ 2.48444641  1.73361328  1.49709126  1.04731282]
 [ 0.66804545 -0.58097793  1.04092235  1.31091014]
 [ 0.54695205 -0.58097793  0.75581678  0.38831953]
 [ 0.30476526 -1.04389617  1.04092235  0.25652088]
 [ 2.24225961 -0.11805969  1.32602791  1.4427088 ]
 [ 0.54695205  0.8077768   1.04092235  1.57450745]
 [ 0.66804545  0.11339944  0.98390123  0.78371551]
 [ 0.18367186 -0.11805969  0.58475344  0.78371551]
 [ 1.27351244  0.11339944  0.92688012  1.17911148]
 [ 1.03132564  0.11339944  1.04092235  1.57450745]
 [ 1.27351244  0.11339944  0.75581678  1.4427088 ]
 [-0.05851493 -0.81243705  0.75581678  0.91551417]
 [ 1.15241904  0.34485856  1.21198569  1.4427088 ]
 [ 1.03132564  0.57631768  1.09794346  1.70630611]
 [ 1.03132564 -0.11805969  0.81283789  1.4427088 ]
 [ 0.54695205 -1.27535529  0.69879566  0.91551417]
 [ 0.78913885 -0.11805969  0.81283789  1.04731282]
 [ 0.42585866  0.8077768   0.92688012  1.4427088 ]
 [ 0.06257847 -0.11805969  0.75581678  0.78371551]]

确定特征向量的数量

协方差矩阵

协方差是衡量两个变量总体误差的期望，用于描述两个变量之间的线性关系程度和方向。两个特征间的协方差值越大，表明其相关性越强。

对于两个随机变量$X$和$Y$，其协方差$Cov(X,Y)$的计算公式为：

$$Cov(X,Y) = E[(X - E[X])(Y - E[Y])]$$

其中，$E[X]$和$E[Y]$分别是$X$和$Y$的期望值（即均值）。

在实际应用中，当我们只有样本数据时，我们通常使用样本协方差来估计总体协方差。对于包含$n$个样本点的数据集，样本协方差$s_{xy}$的计算公式为：

$$s_{xy} = \frac{1}{n-1} \sum_{i=1}^{n} (x_i - \bar{x})(y_i - \bar{y})$$

其中，$x_i$和$y_i$是样本点，$\bar{x}$和$\bar{y}$分别是$X$和$Y$的样本均值，计算公式为：

$$\bar{x} = \frac{1}{n} \sum_{i=1}^{n} x_i$$

$$\bar{y} = \frac{1}{n} \sum_{i=1}^{n} y_i$$

注意，在计算样本协方差时，分母是$n-1$而不是$n$，这是为了得到总体协方差的无偏估计。

以下命令二选一：

构造函数计算协方差矩阵

# 计算特征向量的均值，用于中心化数据
mean_vec = np.mean(X_std, axis=0)

# 计算数据的协方差矩阵，用于理解特征之间的线性关系
# (X_std - mean_vec).T.dot((X_std - mean_vec) )计算的是(X_std - mean_vec)的矩阵乘法
# 除以(X_std.shape[0]-1)是为了获得一个无偏估计
cov_mat = (X_std - mean_vec).T.dot((X_std - mean_vec)) / (X_std.shape[0]-1)

# 输出协方差矩阵，以便于后续分析和使用
print('Covariance matrix \n%s' %cov_mat)

Covariance matrix 
[[ 1.00675676 -0.10448539  0.87716999  0.82249094]
 [-0.10448539  1.00675676 -0.41802325 -0.35310295]
 [ 0.87716999 -0.41802325  1.00675676  0.96881642]
 [ 0.82249094 -0.35310295  0.96881642  1.00675676]]

使用numpy计算协方差矩阵

1	print('NumPy covariance matrix: \n%s' %np.cov(X_std.T))

NumPy covariance matrix: 
[[ 1.00675676 -0.10448539  0.87716999  0.82249094]
 [-0.10448539  1.00675676 -0.41802325 -0.35310295]
 [ 0.87716999 -0.41802325  1.00675676  0.96881642]
 [ 0.82249094 -0.35310295  0.96881642  1.00675676]]

求协方差矩阵的特征向量和特征值。

# 求协方差矩阵
cov_mat = np.cov(X_std.T)

# 求协方差矩阵的特征向量，返回特征向量（eig_vecs）和特征值（eig_vals）
eig_vals, eig_vecs = np.linalg.eig(cov_mat)

print('Eigenvectors \n%s' %eig_vecs)
print('\nEigenvalues \n%s' %eig_vals)

Eigenvectors 
[[ 0.52308496 -0.36956962 -0.72154279  0.26301409]
 [-0.25956935 -0.92681168  0.2411952  -0.12437342]
 [ 0.58184289 -0.01912775  0.13962963 -0.80099722]
 [ 0.56609604 -0.06381646  0.63380158  0.52321917]]

Eigenvalues 
[2.92442837 0.93215233 0.14946373 0.02098259]

肉眼观察Eigenvalues，应当取前2个特征值对应的特征向量，因为其最重要。

创建一个包含特征值和对应特征向量的元组列表。按特征值降序排序这些元组。打印排序后的特征值，确认排序正确。

# Make a list of (eigenvalue, eigenvector) tuples
eig_pairs = [(np.abs(eig_vals[i]), eig_vecs[:,i]) for i in range(len(eig_vals))]
print (eig_pairs)
print ('----------')
# Sort the (eigenvalue, eigenvector) tuples from high to low
eig_pairs.sort(key=lambda x: x[0], reverse=True)

# Visually confirm that the list is correctly sorted by decreasing eigenvalues
print('Eigenvalues in descending order:')
for i in eig_pairs:
    print(i[0])

[(np.float64(2.9244283691111117), array([ 0.52308496, -0.25956935,  0.58184289,  0.56609604])), (np.float64(0.9321523302535062), array([-0.36956962, -0.92681168, -0.01912775, -0.06381646])), (np.float64(0.14946373489813364), array([-0.72154279,  0.2411952 ,  0.13962963,  0.63380158])), (np.float64(0.020982592764271016), array([ 0.26301409, -0.12437342, -0.80099722,  0.52321917]))]
----------
Eigenvalues in descending order:
2.9244283691111117
0.9321523302535062
0.14946373489813364
0.020982592764271016

计算累计变异解释百分比，以评估前几个主成分能解释的总变异比例。最后输出累计变异解释百分比。

# 计算所有特征值的总和
tot = sum(eig_vals)

# 计算每个特征值占总和的百分比，并按降序排序
# 这一步的目的是确定每个特征值在总变异中所占的百分比
var_exp = [(i / tot)*100 for i in sorted(eig_vals, reverse=True)]

# 输出每个特征值的变异解释百分比
print(var_exp)

# 计算累计变异解释百分比
# 这一步是为了了解前几个主成分可以解释多少总变异
cum_var_exp = np.cumsum(var_exp)

# 累计变异解释百分比
cum_var_exp

[np.float64(72.62003332692032), np.float64(23.147406858644143), np.float64(3.711515564584531), np.float64(0.5210442498510259)]

array([ 72.62003333, 95.76744019, 99.47895575, 100. ])

# 演示np.cumsum() 函数的用法
a = np.array([1,2,3,4])
print (a)
print ('-----------')
print (np.cumsum(a)) # 元素的累加和

[1 2 3 4]
-----------
[ 1  3  6 10]

# 绘制特征值的重要性
plt.figure(figsize=(6, 4))

plt.bar(range(4), var_exp, alpha=0.5, align='center',
            label='individual explained variance')
plt.step(range(4), cum_var_exp, where='mid',
             label='cumulative explained variance')
plt.ylabel('Explained variance ratio')
plt.xlabel('Principal components')
plt.legend(loc='best')
plt.tight_layout()
plt.show()

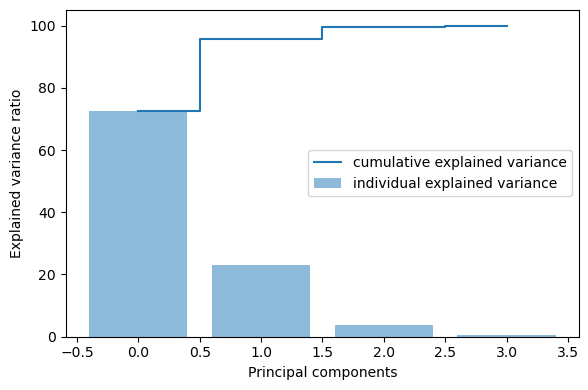
根据上图可以决定取几个特征值进行降维，此例中前两个特征值已经足够（~95.77%）。

# 根据前两个主要成分构造转换矩阵W
# 选择主要成分分析（PCA）得到的前两个特征向量
# 将特征向量重塑为4x1的矩阵形式，以便进行矩阵操作
# 这两个特征向量代表了数据中方差最大的两个方向
matrix_w = np.hstack((eig_pairs[0][1].reshape(4,1),
                      eig_pairs[1][1].reshape(4,1)))

# 打印转换矩阵W，以便于查看和验证结果
print('Matrix W:\n', matrix_w)

Matrix W:
 [[ 0.52308496 -0.36956962]
 [-0.25956935 -0.92681168]
 [ 0.58184289 -0.01912775]
 [ 0.56609604 -0.06381646]]

矩阵降维

# 标准化数据X_std与权重矩阵matrix_w进行点积运算，用于特征提取和数据转换
Y = X_std.dot(matrix_w)

# 输出转换后的数据Y
Y

array([[-2.10795032,  0.64427554],
       [-2.38797131,  0.30583307],
       [-2.32487909,  0.56292316],
       [-2.40508635, -0.687591  ],
       [-2.08320351, -1.53025171],
       [-2.4636848 , -0.08795413],
       [-2.25174963, -0.25964365],
       [-2.3645813 ,  1.08255676],
       [-2.20946338,  0.43707676],
       [-2.17862017, -1.08221046],
       [-2.34525657, -0.17122946],
       [-2.24590315,  0.6974389 ],
       [-2.66214582,  0.92447316],
       [-2.2050227 , -1.90150522],
       [-2.25993023, -2.73492274],
       [-2.21591283, -1.52588897],
       [-2.20705382, -0.52623535],
       [-1.9077081 , -1.4415791 ],
       [-2.35411558, -1.17088308],
       [-1.93202643, -0.44083479],
       [-2.21942518, -0.96477499],
       [-2.79116421, -0.50421849],
       [-1.83814105, -0.11729122],
       [-2.24572458, -0.17450151],
       [-1.97825353,  0.59734172],
       [-2.06935091, -0.27755619],
       [-2.18514506, -0.56366755],
       [-2.15824269, -0.34805785],
       [-2.28843932,  0.30256102],
       [-2.16501749,  0.47232759],
       [-1.8491597 , -0.45547527],
       [-2.62023392, -1.84237072],
       [-2.44885384, -2.1984673 ],
       [-2.20946338,  0.43707676],
       [-2.23112223,  0.17266644],
       [-2.06147331, -0.6957435 ],
       [-2.20946338,  0.43707676],
       [-2.45783833,  0.86912843],
       [-2.1884075 , -0.30439609],
       [-2.30357329, -0.48039222],
       [-1.89932763,  2.31759817],
       [-2.57799771,  0.4400904 ],
       [-1.98020921, -0.50889705],
       [-2.14679556, -1.18365675],
       [-2.09668176,  0.68061705],
       [-2.39554894, -1.16356284],
       [-2.41813611,  0.34949483],
       [-2.24196231, -1.03745802],
       [-2.22484727, -0.04403395],
       [ 1.09225538, -0.86148748],
       [ 0.72045861, -0.59920238],
       [ 1.2299583 , -0.61280832],
       [ 0.37598859,  1.756516  ],
       [ 1.05729685,  0.21303055],
       [ 0.36816104,  0.58896262],
       [ 0.73800214, -0.77956125],
       [-0.52021731,  1.84337921],
       [ 0.9113379 , -0.02941906],
       [-0.01292322,  1.02537703],
       [-0.15020174,  2.65452146],
       [ 0.42437533,  0.05686991],
       [ 0.52894687,  1.77250558],
       [ 0.70241525,  0.18484154],
       [-0.05385675,  0.42901221],
       [ 0.86277668, -0.50943908],
       [ 0.33388091,  0.18785518],
       [ 0.13504146,  0.7883247 ],
       [ 1.19457128,  1.63549265],
       [ 0.13677262,  1.30063807],
       [ 0.72711201, -0.40394501],
       [ 0.45564294,  0.41540628],
       [ 1.21038365,  0.94282042],
       [ 0.61327355,  0.4161824 ],
       [ 0.68512164,  0.06335788],
       [ 0.85951424, -0.25016762],
       [ 1.23906722,  0.08500278],
       [ 1.34575245, -0.32669695],
       [ 0.64732915,  0.22336443],
       [-0.06728496,  1.05414028],
       [ 0.10033285,  1.56100021],
       [-0.00745518,  1.57050182],
       [ 0.2179082 ,  0.77368423],
       [ 1.04116321,  0.63744742],
       [ 0.20719664,  0.27736006],
       [ 0.42154138, -0.85764157],
       [ 1.03691937, -0.52112206],
       [ 1.015435  ,  1.39413373],
       [ 0.0519502 ,  0.20903977],
       [ 0.25582921,  1.32747797],
       [ 0.25384813,  1.11700714],
       [ 0.60915822, -0.02858679],
       [ 0.31116522,  0.98711256],
       [-0.39679548,  2.01314578],
       [ 0.26536661,  0.85150613],
       [ 0.07385897,  0.17160757],
       [ 0.20854936,  0.37771566],
       [ 0.55843737,  0.15286277],
       [-0.47853403,  1.53421644],
       [ 0.23545172,  0.59332536],
       [ 1.8408037 , -0.86943848],
       [ 1.13831104,  0.70171953],
       [ 2.19615974, -0.54916658],
       [ 1.42613827,  0.05187679],
       [ 1.8575403 , -0.28797217],
       [ 2.74511173, -0.78056359],
       [ 0.34010583,  1.5568955 ],
       [ 2.29180093, -0.40328242],
       [ 1.98618025,  0.72876171],
       [ 2.26382116, -1.91685818],
       [ 1.35591821, -0.69255356],
       [ 1.58471851,  0.43102351],
       [ 1.87342402, -0.41054652],
       [ 1.23656166,  1.16818977],
       [ 1.45128483,  0.4451459 ],
       [ 1.58276283, -0.67521526],
       [ 1.45956552, -0.25105642],
       [ 2.43560434, -2.55096977],
       [ 3.29752602,  0.01266612],
       [ 1.23377366,  1.71954411],
       [ 2.03218282, -0.90334021],
       [ 0.95980311,  0.57047585],
       [ 2.88717988, -0.38895776],
       [ 1.31405636,  0.48854962],
       [ 1.69619746, -1.01153249],
       [ 1.94868773, -0.99881497],
       [ 1.1574572 ,  0.31987373],
       [ 1.007133  , -0.06550254],
       [ 1.7733922 ,  0.19641059],
       [ 1.85327106, -0.55077372],
       [ 2.4234788 , -0.2397454 ],
       [ 2.31353522, -2.62038074],
       [ 1.84800289,  0.18799967],
       [ 1.09649923,  0.29708201],
       [ 1.1812503 ,  0.81858241],
       [ 2.79178861, -0.83668445],
       [ 1.57340399, -1.07118383],
       [ 1.33614369, -0.420823  ],
       [ 0.91061354, -0.01965942],
       [ 1.84350913, -0.66872729],
       [ 2.00701161, -0.60663655],
       [ 1.89319854, -0.68227708],
       [ 1.13831104,  0.70171953],
       [ 2.03519535, -0.86076914],
       [ 1.99464025, -1.04517619],
       [ 1.85977129, -0.37934387],
       [ 1.54200377,  0.90808604],
       [ 1.50925493, -0.26460621],
       [ 1.3690965 , -1.01583909],
       [ 0.94680339,  0.02182097]])

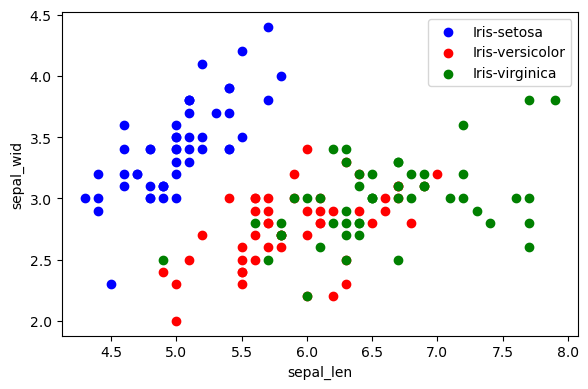
查看降维前的区分表现。

plt.figure(figsize=(6, 4))
for lab, col in zip(('Iris-setosa', 'Iris-versicolor', 'Iris-virginica'),
                        ('blue', 'red', 'green')):
     plt.scatter(X[y==lab, 0],
                X[y==lab, 1],
                label=lab,
                c=col)
plt.xlabel('sepal_len')
plt.ylabel('sepal_wid')
plt.legend(loc='best')
plt.tight_layout()
plt.show()

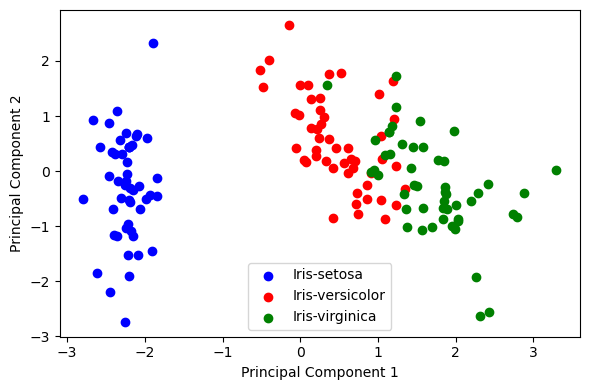
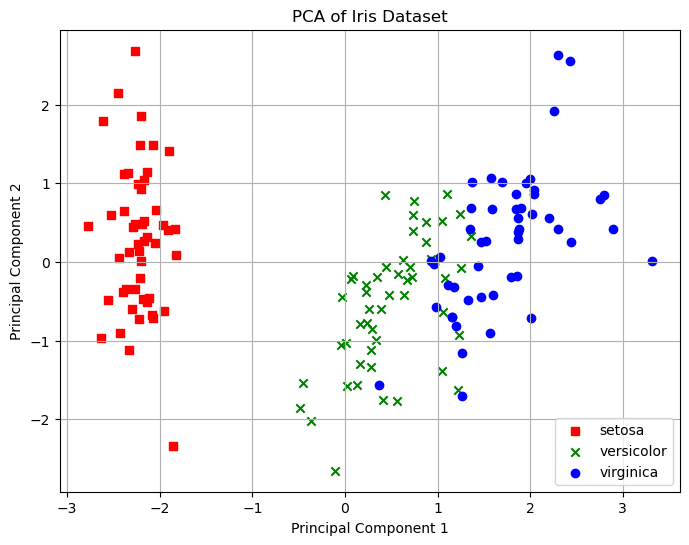
查看降维后的区分表现。

plt.figure(figsize=(6, 4))
for lab, col in zip(('Iris-setosa', 'Iris-versicolor', 'Iris-virginica'),
                        ('blue', 'red', 'green')):
     plt.scatter(Y[y==lab, 0],
                Y[y==lab, 1],
                label=lab,
                c=col)
plt.xlabel('Principal Component 1')
plt.ylabel('Principal Component 2')
plt.legend(loc='lower center')
plt.tight_layout()
plt.show()

利用SK-LEARN PCA进行降维

import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA

# 1. 加载鸢尾花数据集
iris = datasets.load_iris()
X = iris.data
y = iris.target

# 2. 数据标准化
scaler = StandardScaler()
X_std = scaler.fit_transform(X)

# 3. 应用PCA降维
pca = PCA()
X_pca = pca.fit_transform(X_std)

# 4. 计算特征值总和
tot = sum(pca.explained_variance_)

# 5. 计算每个特征值占总和的百分比，并按降序排序
var_exp = [(i / tot) * 100 for i in sorted(pca.explained_variance_, reverse=True)]

# 6. 输出每个特征值的变异解释百分比
print("变异解释百分比:", var_exp)

# 7. 计算累计变异解释百分比
cum_var_exp = np.cumsum(var_exp)

# 8. 输出累计变异解释百分比
print("累计变异解释百分比:", cum_var_exp)

变异解释百分比: [np.float64(72.96244541329987), np.float64(22.850761786701742), np.float64(3.668921889282886), np.float64(0.5178709107154782)]
累计变异解释百分比: [ 72.96244541  95.8132072   99.48212909 100.        ]

由上述结果同样可见，前两个特征向量累计贡献的方差为95.81%，故取前2个特征向量。

# 应用PCA降维到2个主成分
pca = PCA(n_components=2)
X_pca = pca.fit_transform(X_std)

# 4. 绘制PCA图
plt.figure(figsize=(8, 6))

# 为不同的类别绘制不同颜色的点
colors = ['r', 'g', 'b']
markers = ['s', 'x', 'o']

for idx, color, marker in zip(range(3), colors, markers):
    plt.scatter(x=X_pca[y == idx, 0], 
                y=X_pca[y == idx, 1],
                c=color, 
                marker=marker,
                label=iris.target_names[idx])

# 添加标题和标签
plt.title('PCA of Iris Dataset')
plt.xlabel('Principal Component 1')
plt.ylabel('Principal Component 2')
plt.legend()
plt.grid(True)

# 显示图形
plt.show()

加关注

关注公众号“生信之巅”，获取更多教程。

敬告：使用文中脚本请引用本文网址，请尊重本人的劳动成果，谢谢！Notice: When you use the scripts in this article, please cite the link of this webpage. Thank you!

了尘兰若的小坑

分享微生物生物信息学分析方法，欢迎加入QQ群交流945751012，不接受群内广告！

前言